選題背景
英國數學家Alfred North Whitehead提出“數學的本質不僅是邏輯,更是模式與美的科學”,強調數學結構本身具有和諧之美,而審美直覺能促進數學的創造性思維,可見數學與美學原本就具有深層聯系。當下教育改革提倡“五育融合”,如何將美育滲透到數學教學中,提升學生的數學思維和審美價值是重要的研究課題。普通高中數學“圓錐曲線”包含豐富的美學元素,是展現數學美的重要載體,也是利用美學促進數學發現、激發學生數學興趣的巧妙著力點。但目前課堂教學中,教師注重知識的教授、運算技巧的講解,常常忽視了美學與數學的交互。
《橢圓及其標準方程》作為“圓錐曲線”教學內容的起始課,在研究策略和思想方法上起著重要的引領作用,且具有豐富的美育要素可挖掘。例如,章頭語圓錐曲線的原始定義可以體現圓錐曲線的統一美,從三維空間的原始定義到二維平面的第一定義的銜接可以感悟多種定義的和諧美等。因此,本文以《橢圓及其標準方程》為例進行美育浸潤的教學設計實踐。
教學目標
1.經歷從具體情境抽象出橢圓的過程,掌握橢圓的定義及其標準方程。
橢圓的定義有多種呈現形式,本課例根據教材主要呈現圓錐曲線的原始定義和第一定義,從三維空間中讓學生感受圓錐曲線的統一性,從二維平面中讓學生理解橢圓第一定義的嚴謹性。
2.通過繪制橢圓的過程嚴謹認識橢圓定義,經歷方程的推導過程培養直觀想象、邏輯推理、數據運算等核心素養。
通過感受—發現—驗證定義,體會數學定義概念的簡潔、嚴謹、統一,是數學中美學的體現;經歷建系—設點—化簡方程,用美學啟發數學思維,激發創造力,落地核心素養。
3.感受并發現數學研究過程中美的呈現,對數學的內在結構和思想的理性美充滿好奇與欣賞。
利用平面截圓錐的模型展示、旦德林雙球模型展示以及拉線作圖的實踐操作,感受數學的模型美、形狀美,激發學生學習的興趣和探索的欲望。
教學設計創新
1.引入方式的創新。
本課例沒有直接引入“拉線作圖”情境得出橢圓定義,而是選用兩個情境層層遞進引出橢圓定義。一是利用章頭語介紹圓錐曲線統一定義,引出“橢圓”;二是利用點光源照射球實驗引出“焦點”,并借助旦德林雙球模型展示二維平面橢圓上的點與兩個焦點之間的關系。這一設計實現了橢圓定義從三維空間到二維平面的平穩過渡,使學生的認知理解更加自然和順暢。
2.美學引領問題串的推導方式創新。
課例中并未采用以教師為主導的方式進行方程的推導,而是通過學生小組合作的形式,配套具有指引性的問題串引導學生進行方程化簡,發現數學的對稱美、簡潔美。
3.豐富動態展示的技術創新。
課例多處設置了動態模型、動手實驗,旨在提升學生學習興趣的同時,借助動態生成的過程激發學生的創造力,引導學生體悟感性美到理性美的升華。
教學實施
1.立足全章,構建定義—感受形狀美、模型美
師:圓錐曲線的名稱由何而來?它與圓錐有什么聯系?
情境1:GGB動態展示平面截圓錐模型(見圖1)
師:用一個垂直于圓錐的軸的平面截圓錐,截口曲線是一個圓,如果改變圓錐的軸與平面形成的角,會得到怎樣的曲線?
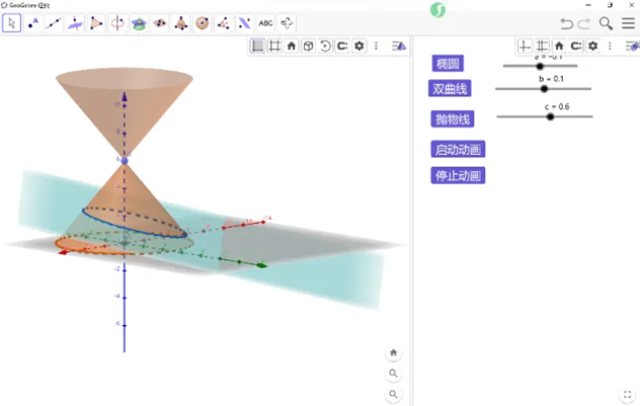
圖1
【師生互動】用不垂直于圓錐曲線的軸的平面截圓錐,直觀觀察得到不同曲線,有橢圓、雙曲線、拋物線,統稱為圓錐曲線,引導學生理解曲線名稱的來源和三種曲線之間必然存在的緊密聯系。
師:在之前直線與圓的學習研究中,我們體會了坐標法研究幾何的魅力與威力,現在延續這種思路,繼續研究橢圓。
情境2:生活實驗模擬旦德林雙球模型
【師生互動】教師用手電筒照射桌面放置的乒乓球,學生觀察球的影子形狀。當光線垂直于桌面,影子為圓形;當光線斜射小球時,影子為橢圓形。影子為圓形時,圓心就是球與桌面的切點,影子邊緣上的點到切點距離不變,是圓的定義。啟發學生思考影子為橢圓形時,此時的切點到影子邊緣的距離是否不變。
師:當影子為橢圓形時,切點在一邊,這個切點位置是做不到距離不變的。1個切點辦不到,猜測可能會有幾個?
【模型介紹】光線是無限延展的,延展開的光線是一個圓錐,小球是與圓錐內切,桌面相當于一個平面截圓錐且與小球相切,事實上,下方也有一個大的球與圓錐和平面同時相切。這個模型就是著名的旦德林雙球模型,這里呈現的兩個切點就是橢圓的關鍵要素“焦點”(見圖2)。
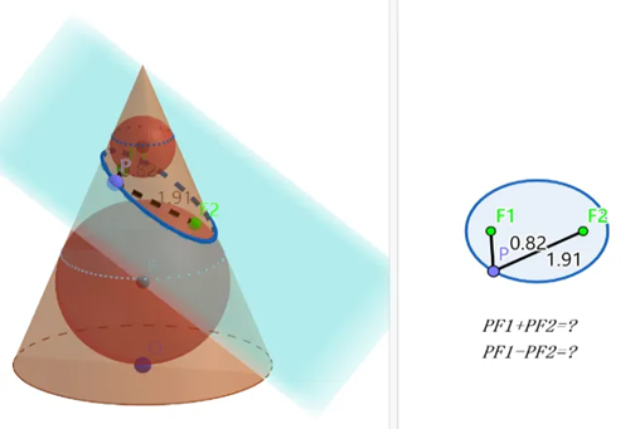
圖2
師:兩個焦點與橢圓上的點有什么量化關系?
【師生互動】教師拖動P點運動,引導學生發現距離之和不變。數據度量直接證明橢圓上的點到兩個焦點的距離之和為定值,教師可從幾何角度簡單說明定值的原因。
2.歸納定義,推導方程—發現嚴謹美、簡潔美
活動1:拉線作圖驗證第一定義
師:橢圓上的點到兩個焦點的距離之和為定值,反過來,若滿足到兩定點距離之和為定值,點的軌跡一定是橢圓嗎?接下來自己動手驗證,請按照教材的探究畫一畫。
【師生互動】教師引導學生在白紙上用釘子固定兩個點,并用一個繩子連接,進行拉線作圖(見上頁圖3),然后改變兩個點的距離,研究觀察。
師:在作圖過程中,什么時候軌跡是橢圓?線段關系如何?
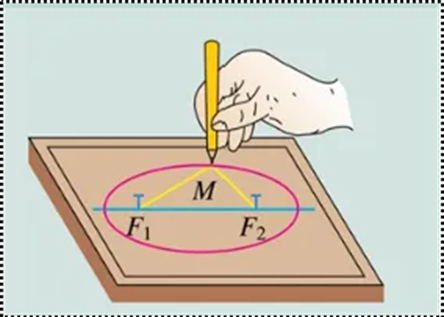
圖3
生:三個點可以形成三角形時,要滿足PF1+PF2>F1F2。
師:改變兩點間距離后發現了什么?
生:當兩點間距離和繩子長度一樣時,軌跡就是線段F1F2;當距離超過繩子長度時就畫不出來,不存在。
【定義析出】平面內到兩個定點F1F2的距離和等于常數2a(2a>|F1F2|)的點的軌跡叫作橢圓。
活動2:小組合作推導橢圓方程
師:請小組合作,根據以下幾個問題,通過坐標法探索橢圓的方程。
問題1:如何用數學符號語言嚴謹刻畫橢圓的定義?
問題2:如何建立恰當的直角坐標系,使設點更加合理?
問題3:如何化簡方程,使方程便于記憶,稱之為“標準方程”?
【師生互動】利用定義,學生很快得出符號語言的表述:PF1+PF2=2a(2a>F1F2)。追求簡潔性與對稱性,一般以F1F2為x軸,線段F1F2的中點為原點建立直角坐標系,設點P(x,y),F1(-c,0)F2(c,0),利用兩點間距離公式,得出方程:
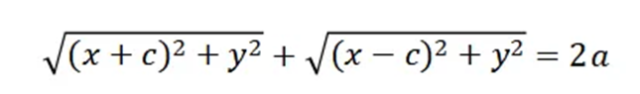
此時的方程不具有美觀性和可記憶性,啟發學生通過移項、平方、化簡尋求簡潔美,得到
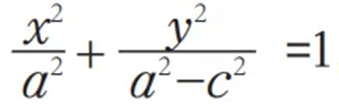
但式子結構不具備對稱美,繼續優化引入b,
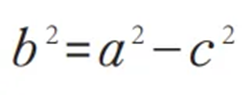
并利用關系找到b在幾何圖形中的位置,最終得出
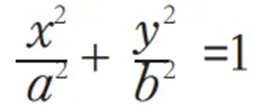
3.回顧反思,提煉升華—欣賞過程美、方法美
師:本節課學習了橢圓的定義及其標準方程,回顧是如何一步步探究的?
生:通過平面截圓錐發現圓錐曲線的存在,找到橢圓;旦德林雙球模型引出焦點發現了橢圓上的點與兩個焦點的距離之和為定值,拉線作圖嚴謹驗證橢圓軌跡形成的條件,得出橢圓的第一定義,最后通過坐標法得出標準方程。
師:通過數學的視角,我們在橢圓形中感受到哪些美學瞬間?
生:橢圓的形狀具有對稱美,方程有簡潔美和對稱美,圓錐曲線的原始定義具有統一美,橢圓的第一定義具有嚴謹美……
【PPT呈現】(見圖4)
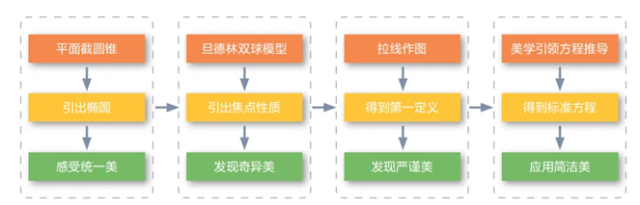
圖4
4.及時鞏固,熟練應用—拓展思維美、應用美
教師可通過以下例題幫助學生及時練習并鞏固所學知識。
例1:已知橢圓經過點
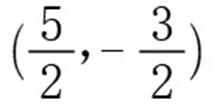
且它的兩個焦點坐標分別為(-2,0),(2,0),求它的標準方程?
例2:如果橢圓
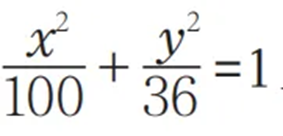
上的一點P與焦點F1的距離為6,那點P與另一個焦點F2的距離是多長?
(李婷 作者單位系浙江省長興縣太湖高級中學)
《人民教育》2025年第15-16期,原文有修改
工信部備案號:京ICP備05071141號
互聯網新聞信息服務許可證 10120170024
中國教育報刊社主辦 中國教育新聞網版權所有,未經書面授權禁止下載使用
Copyright@2000-2022 www.junhanjc.com All Rights Reserved.